Thèse
de Doctorat de l'Université Pierre et Marie Curie,
présentée par Olivier LAS VERGNAS
sous la direction de Jean-Paul BENZECRI,
Professeur à l'Université Pierre et Marie Curie
soutenue à Paris, le 25 juin 1990, devant le jury composé de :
Bruno
MORANDO, Bureau des Longitudes, président et
Jean-Paul BENZECRI, Laboratoire de Statistique de l'UPMC,
Carlos JASCHEK, Centre de Données Stellaires de Strasbourg,
Jean-Pierre VERDET, Observatoire de Paris, examinateurs.
[télécharger
ICI la thèse en texte intégral (archives ouvertes HAL, format pdf 2.5 Mo)]
[accéder
à un article de synthèse sur le sujet (sur HAL, BduCDS, 1989)]
[accéder au rapport de soutenance de thèse (juin 1990)]
Résumé général Les étoiles brillantes ont-elles des variations séculaires d'éclat ? Bien que plusieurs astronomes aient étudié ce sujet au cours des siècles écoulés, aucune réponse satisfaisante n'y a été donnée. Il y a un siècle, C. Flammarion rassembla les anciennes estimations et les publia dans son ouvrage Les étoiles et les curiosités du ciel. Il était évident de son point de vue qu'un grand nombre d'étoiles avaient eu des variations séculaires. Pickering (1895) et Zinner (1926) publièrent deux autres compilations de catalogues. Ils ne partageaient pas le point de vue de Flammarion, mais ne purent interpréter l'information contenue dans les données. Il n'y a pas eu d'étude plus récente sur ce sujet. De nouvelles méthodes d'analyse -comme l'analyse factorielle des correspondances- ont été créées ces dernières années, qui permettent d'étudier de manière approfondie de grands tableaux de données. La finalité du travail présenté ici est de voir si ces méthodes peuvent nous aider à résoudre ce problème des variations séculaires. La compilation des catalogues originaux permet de constituer un tableau de données intégrant des éléments "signatures" des diverses causes susceptibles d'expliquer les écarts d'éclats (des causes astrophysiques à la non-fiabilité des données). Plusieurs analyses factorielles, utilisant des codages spécifiques des données, comme "l'écart aux valeurs attendues" ou le "codage flou en magnitude entière", créés pour limiter les différences de notations entre les observateurs sont effectuées. Il n'en ressort pas de "signatures" significativement corrélées avec les écarts d'éclats ; en particulier, il n'y a pas d'effet de couleur constaté. Il semble y avoir globalement "mémoire" des éclats d'un catalogue sur l'autre. Seul échape à cette règle, le catalogue de Sir William Herschel, qui est également le seul à contenir des comparaisons d'éclat et non pas des valeurs de magnitude. Cela amène à se demander si il n'aurait pas été protégé de cet effet de "mémoire" à cause de sa différence de notation. Ce travail ne clôt pas la question. Il se termine par la définition de nouvelles analyses à mettre en place : pour tirer des conclusions astrophysiques, il peut être utile de tester des traitements combinant l'analyse factorielle et l'analyse de Fourier. De tels traitements permettront de se débarasser de l'information de phase et d'effectuer des études de corrélation de périodes.
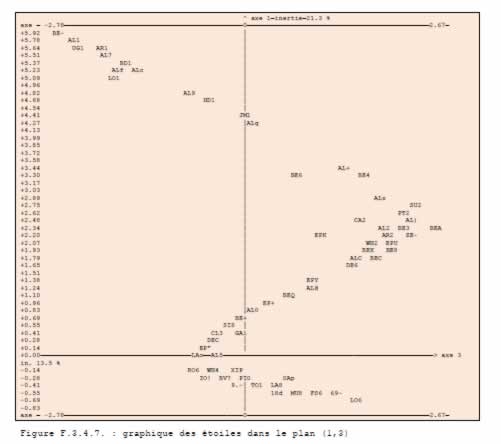
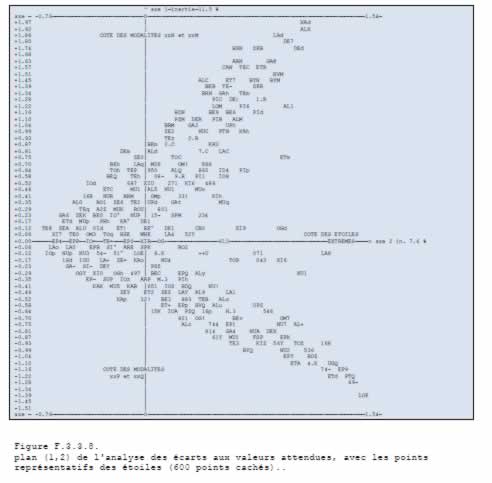
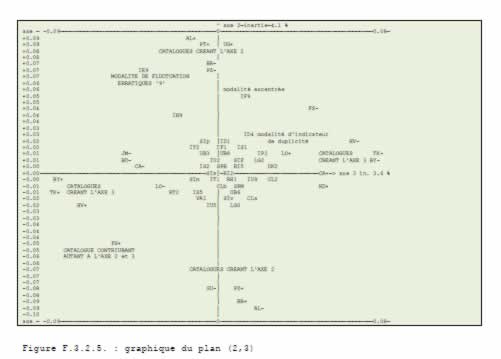
Principes méthodologiques Les méthodes d'analyse de données, en particulier les analyses factorielles et les classifications automatiques permettent aujourd'hui d'analyser des grands tableaux de données comme ceux qui regroupent l'information disponible sur notre problème. Le principe de ces méthodes est de partir sans a priori sur les données et de les décrire en analysant la hiérarchisation de l'information présente dans les données. Pour ce faire, les analyses factorielles étudient l'inertie du nuage de points ayant pour coordonnées les valeurs présentes sur les lignes du tableau de données. Ces méthodes correspondent donc à la stratégie que nous avons choisi d'employer. La "morphologie du nuage" et la répartition des points sur chacun de ces axes d'inertie permettent alors, de rendre lisible et hiérarchisée l'information contenue dans le tableau. Mathématiquement, après avoir centré et réduit le tableau de données que l'on a affecté d'un système de masse (par exemple, les sommes marginales de chaque ligne), on calcule la matrice d'inertie associée et on la diagonalise (la répartition de l'information selon les différents axes est représentée par l'histogramme des valeurs propres). On effectue alors un changement de base selon ses vecteurs propres, c'est-à-dire selon les axes principaux d'inertie du nuage de points. On projette alors les points figurant chaque ligne sur les nouveaux axes. L'ensemble de l'information est conservé, mais celle-ci est maintenant hiérarchisée, axe d'inertie par axe d'inertie. L'histogramme des valeurs propres permet de voir le type de répartition de l'information entre les différents axes et l'étendue en dimension de celle-ci. Le premier axe d'inertie oppose les points, c'est-à-dire les lignes du tableau (dans notre cas les étoiles) ayant les plus grandes distances ou "différences". La première valeur propre d'inertie, (associée à ce premier axe) mesure la quantité d'information présente le long de cet axe, c'est-à-dire dans cette opposition. On analyse ainsi les différents axes, en reconstituant progressivement la totalité des données. Plusieurs méthodes d'analyse des correspondances existent, qui diffèrent par le type de représentation de l'information, c'est-à-dire de métrique, ou de système de masse qu'elles utilisent. L'analyse factorielle des correspondances développée par Jean Paul Benzecri et ses collaborateurs est la méthode que nous avons choisi d'utiliser, car la métrique qu'elle emploie (métrique du chi-deux : chaque ligne est affectée d'une masse qui est sa somme marginale, le tableau étudié est le tableau des profils des lignes) permet de représenter dans le même espace à la fois les deux nuages de points associés aux lignes et aux colonnes du tableau de données ; elle est par ailleurs très agréablement complétée par des outils de classification ascendante hiérarchique (CAH) qui permettent d'apporter des visions complémentaires, en particulier en construisant des arbres de classification des lignes ou des colonnes. Pour chaque point représentatif des lignes ou des colonnes du tableau de données, nouvel axe par nouvel axe, on s'intéresse à ses nouvelles coordonnées, au cosinus carré de l'angle avec l'axe (ce qui est équivalent à un coefficient de corrélation), ainsi qu'à sa contribution à l'inertie expliquée par l'axe (c'est-à-dire à sa contribution à la création de l'axe). Le programme, que nous avons écrit en pascal pour effectuer ces analyses, publie en plus des graphiques des plans principaux, ces données dans un format compatible avec un programme de base de données relationnelle, ce qui permet de les exploiter de manière très approfondie (tri, filtrage, mise en relation par exemple). Deux contraintes particulières sur les données sont à signaler : d'une part, les tableaux ne peuvent comporter de cases vides et d'autre part, seules des valeurs positives sont permises. Afin d'utiliser l'AFC pour étudier notre problème, nous devons constituer -à partir des données d'éclat- des tableaux vérifiant ces caractéristiques. Il y a deux types de mise en forme des données possibles : constituer un tableau quantitatif ou un tableau qualitatif (constitué de 1 ou de 0). Nous avons également à tenir compte des problèmes de masse de chaque ligne : compte tenu de la métrique du chi-deux employée par l'AFC, cette méthode accorde une importance plus grande aux lignes de somme marginale élevée. Si nous utilisons des tableaux quantitatifs et souhaitons équilibrer la contribution de chaque ligne au calcul de l'inertie, nous devons transformer le tableau pour assurer à chaque ligne une somme marginale égale. Pour ce faire, on peut dédoubler chaque ligne, en lui adjoignant un tableau de complément. A chaque valeur fij, on fait correspondre une valeur dédoublée k-fij, avec k>=max(fij). Lorsque nous analyserons des tableaux quantitatifs de magnitude, nous utiliserons cette solution. Par l'AFC, il est tout autant possible d'analyser des tableaux contenant des mesures quantitatives (comme la magnitude par exemple), que des indications qualitatives, du type vrai-faux, ces deux types ne pouvant être mélangés. Un cas particulier de la deuxième catégorie de tableau est constituée par les tableaux "disjonctifs" ; plusieurs variables constituent les colonnes : elles sont toutes découpées en plusieurs modalités, dont une et une seule est vraie par individu. Une famille de solutions intermédiaires existe cependant, sur laquelle nous reviendrons : il s'agit de la famille des codages flous, qui permettent de manipuler de manière très élégante et fort efficace des concepts hybrides entre le quantitatif et le qualitatif. Lors d'une analyse factorielle, on peut rajouter des données "supplémentaires", c'est-à-dire que l'on ne fait pas intervenir dans le calcul de l'inertie, mais que l'on projette sur les axes. On peut ainsi introduire des descriptifs physiques des étoiles. Dans le cas d'un tableau disjonctif (ou plus généralement de tout tableau qualitatif), on pourra introduire des données supplémentaires qualitatives. Dans le cas d'un tableau quantitatif, afin de pouvoir interpréter les projections des points supplémentaires, il ne faut pas rendre inhomogènes les codages : il faudra introduire des étoiles fictives, centres de gravité de classes "types" d'étoiles, qui, elles, se projetteront en des points significatifs du comportement moyen de cette classe d'astre. Repères bibliographiques Flammarion, Camille. Les étoiles et les curiosités du ciel. Paris : Marpon et Flammarion, 1882 [reimpr, Pecker J.C. : Paris : Flammarion, 1981 Benzécri, Jean-Paul. Histoire et préhistoire de l'analyse des données Paris : Dunod (collection "Pratique de l'analyse des données"), 1981 Benzécri, Jean-Paul et al. Analyse des correspondances. Paris : Dunod (collection "Pratique de l'analyse des données"), 1979. Benzécri, Jean-Paul et al. Abrégé Théorique et Etude de cas modèle. Paris : Dunod (collection "Pratique de l'analyse des données"), 1979 |